日期：2024-10-14 浏览量：
日前，贵州理工学院土木工程学院李永辉老师以第一作者身份在国际权威期刊??《COMPUTERS AND GEOTECHNICS》（TOP期刊，中科院一区，影响因子IF=5.3）上发表题为《An anisotropic elastoplastic strong discontinuity model for shear failure inanisotropic rock masses》研究论文，并被Web of Science数据库检索。
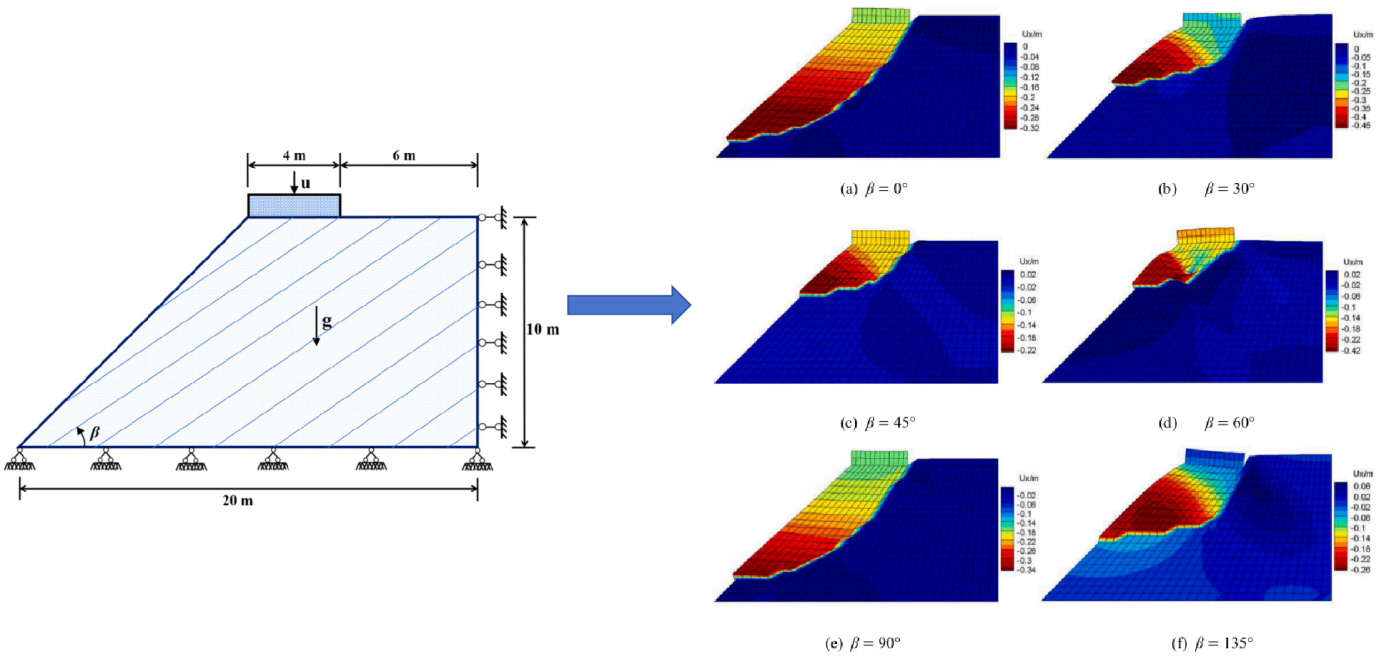
该研究提出了一种新型的各向异性弹塑性强不连续有限元法（SD-FEM），用于分析各向异性岩体中完整的渐进剪切破坏过程。岩体滑移前的变形特性通过结合微观结构张量方法的弹塑性公式来描述。进行各向异性不连续分叉分析，以判断滑移线的起始条件和传播方向。此外，利用在不连续面上推导出的各向异性应力-位移关系来描述与滑移相关的破坏后响应。为了便于数值实现，导出了控制方程的弱形式和矩阵形式。并且，采用了静力凝聚技术来消除单元中附加的不连续位移自由度，这一技术使得各向异性SD-FEM在现有的有限元程序中容易实现，并节省了计算成本。
通过两个数值示例，即各向异性岩体的单轴压缩试验和各向异性岩质边坡的加载问题，展示了各向异性弹塑性SD-FEM模型在分析各向异性岩体力学特性方面的显著优势。该模型不仅能反映岩体的各向异性力学特性，还能准确模拟岩体从均匀变形到滑移破坏的完整渐进破坏过程。值得注意的是，滑移量（即不连续位移）随着施加荷载的增加呈线性增长，突显了岩体的弹-脆性变形特性。此外，即使在软化阶段，全局刚度矩阵的特征值仍然保持正值，这使得数值计算可以继续进行，并确保了网格无关的数值解，这表明各向异性SD-FEM可以在应变软化发生时正则化边值问题的不适定性，解决了经典FEM数值计算中网格依赖的问题。
李永辉，博士，贵州理工学院土木工程学院教师。博士毕业于大连理工大学岩土工程专业，主要研究方向为岩土工程数值计算、智能监测以及地质灾害评估。共发表学术论文10余篇，其中以第一作者（通讯作者）发表中科院一区Top期刊SCI论文3篇。
一审：姚楠
二审：巫敏
三审：李朋
地址：贵州省贵安新区党武镇博士路 邮编：550025 电话：0851-88121166 传真：88121166
?贵州理工学院版权所有 ICP备案号：黔ICP备13005433号-1
